PMAC 2024 Workshop
Cross-Validation of SPH-based Machine Learning Models using the Taylor-Green Vortex Case
As presented at the Particle Methods and Applications Conference 2024 co-hosted by LANL and SPHERIC.
The Slides: https://docs.google.com/presentation/d/1W1yhR9dHK5ysy2fIDsSPK6_JHSIFXYCW/edit#slide=id.p1
Our recent (May 2024) paper published at ICLR 2024: https://openreview.net/forum?id=HKgRwNhI9R
Last Years live demo from SPHERIC 2023 (Rhodes) using Continuous Convolutions to learn a kernel function: https://colab.research.google.com/drive/1wdJoWvu1U5pftkjpjG0gb0ldSh5-CgDX (if the code doesnt work contact me please)
If you have any suggestions or ideas or collaboration ideas contact me via email at rene.winchenbach at tum.de or find me on linked in: https://www.linkedin.com/in/rene-winchenbach-56a217257/
Interesting reads if you are interested in more machine learning in physics
- Learning Lagrangian Fluid Mechanics with Continuous Convolutions: the baseline of our current research https://openreview.net/forum?id=B1lDoJSYDH
- Guaranteed Conservation of Momentum for Learning Particle-based Fluid Dynamics: a follow up work on the prior paper that builds in hard constraints to ensure conservation of momentum https://arxiv.org/abs/2210.06036
- Physics informed machine learning with Smoothed Particle Hydrodynamics: Hierarchy of reduced Lagrangian models of turbulence: The paper presented by Michael Woodward at PMAC https://arxiv.org/abs/2110.13311
- Message-Passing Neural PDE Solvers: A state of the art graph based neural network approach to solving generic PDEs https://openreview.net/forum?id=vSix3HPYKSU
What we plan on doing next:
- Hybrid solvers, e.g., low order SPH method + Neural network corrections to achieve higher order accuracy
- Investigating more general Radial Basis Function Networks for particle mechanics
- Learning specific subparts of an SPH simulation that are really expensive, e.g., the recent iterative particle shifting method
- Publishing our dataset (after some more work to make it more representative) as a dataset paper
Finally an interesting example like mentioned
Heres an example from a ground truth trajectory
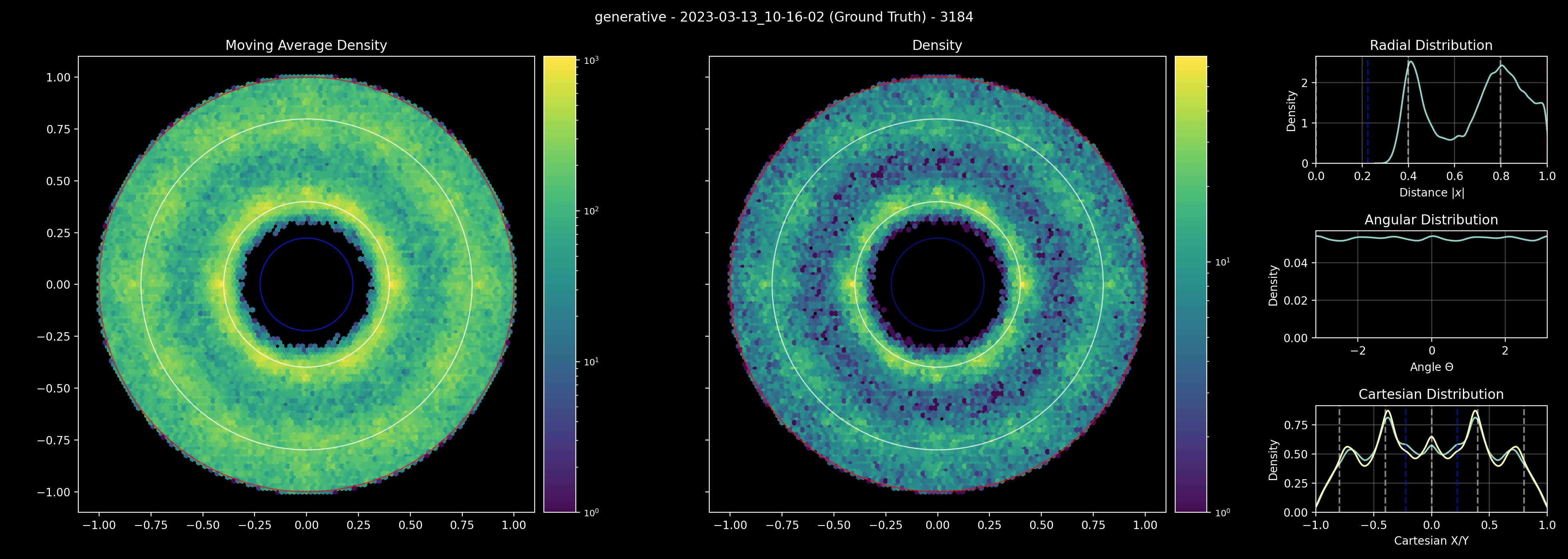
Shown here is a distribution of relative particle positions sampled over a few timesteps (left) and for a single step (right). In the ground truth we see a clear formation of two rings at $\Delta x$ and $2\Delta x$ with a minimum particle separation but an otherwise uniform distribution. Now consider a machine learning trajectory:
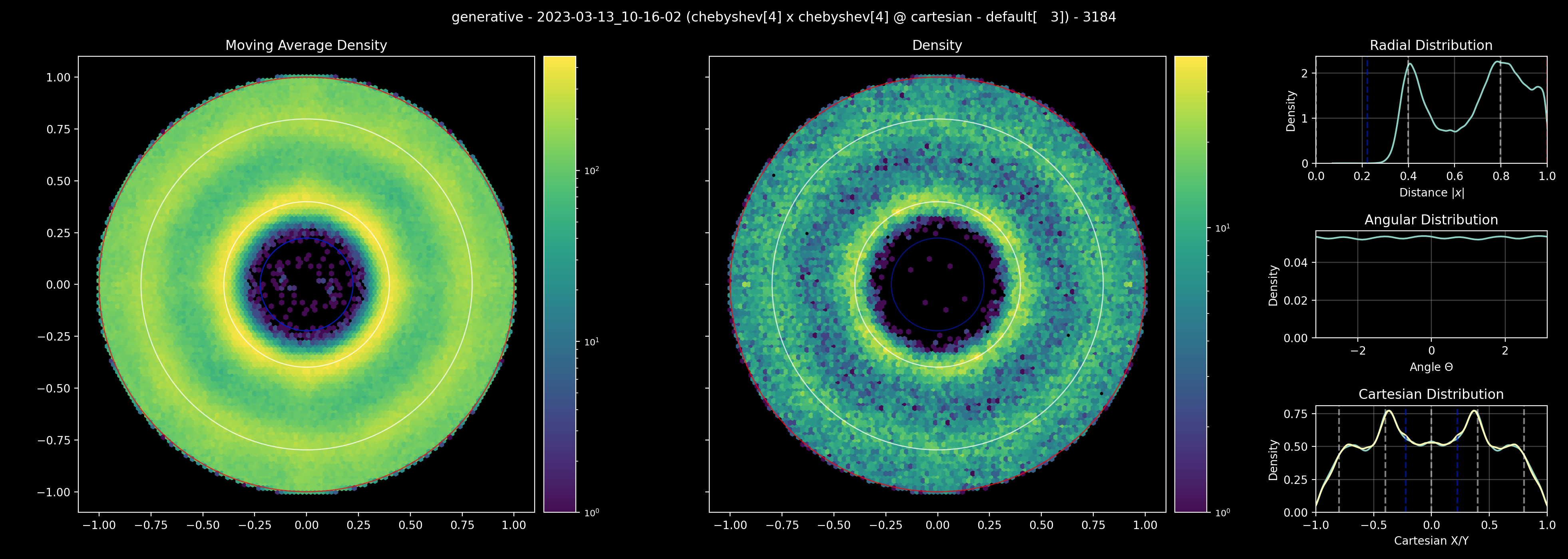
Here we still see the two rings and uniformity but the minimum particle separation is lower. This can often lead to issues during inference as those distributions are not included in the training data, albeit this can be reduced in impact by using unroll noise and data augmentation (to an extent). Now consider this method:
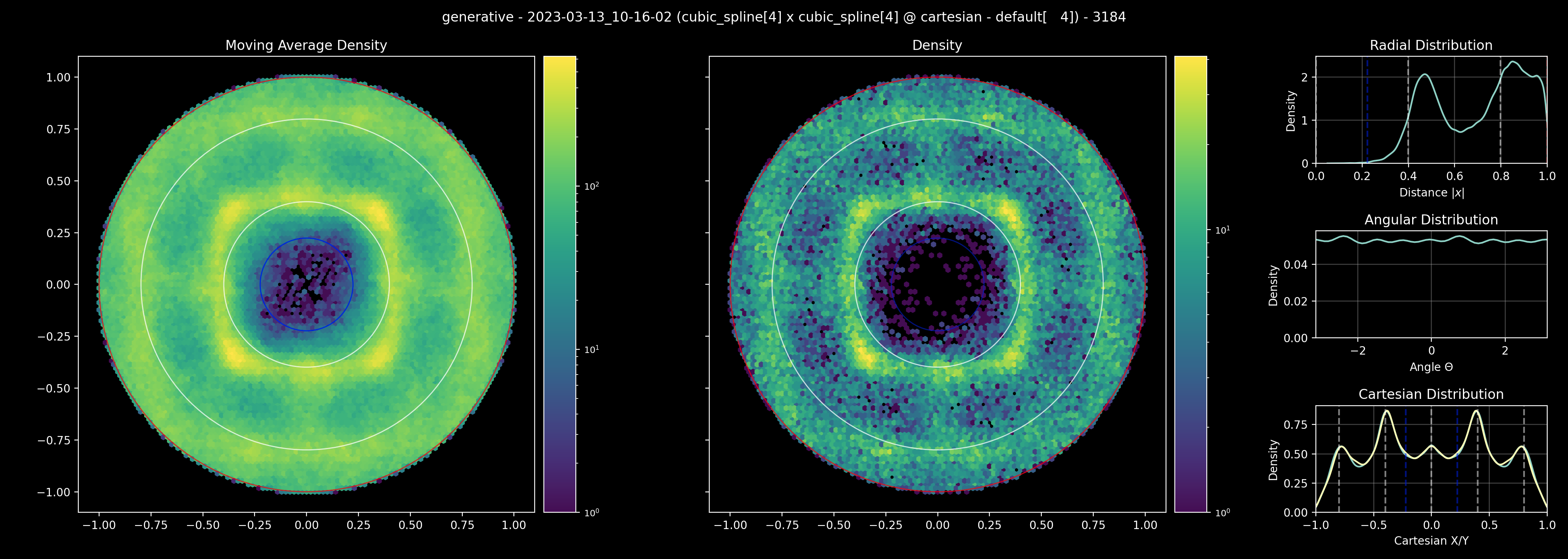
Which shows a highly biased distribution that aligns much closer to a rectilinear grid than an isotroptic distribution with a much lower minimum distance between particles. While this looks worse, and arguably is, this method is more stable in a lot of cases as this distribution acts as a stabilizing measure by regularizing the particle positions, similar to particle shifting. Note that the real reason we got these results was that the method in the last picture wasnt implemented properly and the bug lead to an interesting and, somewhat, improved result.